Childhood's END is the possibility and the actuality of the end of numbers in Name, Term, Essence, and in essence is unknowable. Childhood's End is one of the smaller layers of the Universe.

A number is a mathematical object used to count, measure, and label. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called numerals. In addition to their use in counting and measuring, numerals are often used for labels, ordering, and for codes.

Numbers that have no hold on their former contents, no continuing conception of the reality of that which once was to it all that was real is contained within Childhood's END.

• All nonmanifest numbers are contained within Childhood's END.
• All unreachable unmanifest numbers are contained within Childhood's END.
• All uncollapseable numbers are contained within Childhood's END.
• Childhood's END contains all numbers of pure absoluteness void of all connection with this world of apparent manifestation, incapable of supporting cognition or dynamic maintenance of it that gives it a reality—or, if there is such a cognition, it must be of the nature of an Is that is not.
• All numbers that are progressively seizing, constantly interpreting existence, and all numbers that are subjectively building up in ourselves of this manifestation of the Unmanifest exist here.
• All Numbers that are Absolute, and because they are Absolute, the numbers cannot be reduced to terms of knowledge exists here.
• All numbers in existence or nonexistence that are symbols of the Absolute created in self-consciousness exist here.

All number entities, number abstractions, number possibilities, and number impossibilities exist within Childhood's END. Numbers that operate "beyond" or "outside" are within Childhood's END. All arrangments of possible numbers and impossible numbers are here.

• All numbers and transcendental numbers that are essentially indescribable, superseding the property of being described are here.
• All transcendental beings in connection with statements applicable to being of layers are encompassed and surpassed here.
• All arrangements of statements or that which is impossible to be considered a statement that surpasses definition or size is encompassed and superseded here.

Childhood's END contains the ⛎numbers that actualize anything and everything -- be it physical (matter, energy, the space-time continuum, etc.); or metaphysical (layers of the soul, types of mind, interpretations of life, layers of death, logic, metalogic, aspects of reality, Platonic forms and Jungian Archetypes). These ⛎numbers have complete control and precision over absolutely everything and whatever is beyond. These ⛎numbers can create and command the totality of all things to the highest pinnacle; there is nothing imaginable and unimaginable that these numbers cannot perfectly actualize. Just a mere ⛎number here completely transcends the concept of totality and views it all as just a nonexistent thought.

• For every type of number, there is an Illimitable/Limitless/Ultimate/Unlimited/Unparalleled/Unrestricted Raw Number that is present here.
• Every single ⛎number is an Omniversal void itself and is infinitely above every being that has a type (metaphysical) or property and contains infinite multiverses within itself.
• Every single ⛎number is free from all laws and limitations and is immeasurable and constantly rising.
• Every single ⛎number is the embodiment of storytelling.
• Every single ⛎number possesses powers beyond all hope of measure.

Childhood's END contains transhierarchical and transcendental higher numbers such as unspeakable numbers and numbers beyond boundlessness. For each number, there is an End of Infinity within it.

• Unfathomable transhierarchical numbers and transcendental higher Unfathomable numbers exist here.
• Incalculable transhierarchical numbers and transcendental higher Incalculable numbers exist here.
• Measureless transhierarchical numbers and transcendental higher Measureless numbers exist here.
• Boundless transhierarchical numbers and transcendental higher Boundless numbers exist here.
• Incomparable transhierarchical numbers and transcendental higher Incomparable numbers exist here.
• Innumerable transhierarchical numbers and transcendental higher Innumerable numbers exist here.
• Unaccountable transhierarchical numbers and transcendental higher Unaccountable numbers exist here.
• Unthinkable transhierarchical numbers and transcendental higher Unthinkable numbers exist here.
• Immeasurable transhierarchical numbers and transcendental higher Immeasurable numbers exist here.
• Uncollapseable transhierarchical numbers and transcendental higher Uncollapseable numbers exist here.
• Unspeakable transhierarchical numbers and transcendental higher Unspeakable numbers exist here.
• Impassable Unspeakable transhierarchical numbers and transcendental higher Impassable numbers exist here.
• Untold transhierarchical numbers and transcendental higher Untold numbers exist here.

All numbers (abstractions) and their subtypes and subclasses that can be linked to Fiction, Nonfiction, Transfiction, Fanfiction, Metafiction, Patafiction, Interfiction, Personal Fiction, Impersonal Fiction, Incompatibilism Fiction, Impossible Fiction, Speculative Fiction, Xenofiction, Universal Genre, Universal Trope, Paratexts, Memetic Fiction, Transformation Fiction, and a priori and a posteriori Fiction come to an end here.

Extensions of the concept

Zero

The use of 0 as a number should be distinguished from its use as a placeholder numeral in place-value systems. The rules of using zero with negative and positive numbers encompass such as "zero plus a positive number is a positive number, and a negative number plus zero is the negative number."

Negative numbers

In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is less than zero. Negative numbers are often used to represent the magnitude of a loss or deficiency. If a quantity, such as the charge on an electron, may have either of two opposite senses, then one may choose to distinguish between those senses—perhaps arbitrarily—as positive and negative. Negative numbers are used to describe values on a scale that goes below zero. The laws of arithmetic for negative numbers ensure that the common-sense idea of an opposite is reflected in arithmetic.

• Every real number other than zero is either positive or negative. The non-negative whole numbers are referred to as natural numbers (i.e., 0, 1, 2, 3...), while the positive and negative whole numbers (together with zero) are referred to as integers. (Some definitions of the natural numbers exclude zero.)

Rational numbers

A rational number is a type of real number, which is in the form of p/q where q is not equal to zero. Any fraction with non-zero denominators is a rational number. 

A rational number is a number that can be expressed as a fraction with an integer numerator and a positive integer denominator. Negative denominators are allowed but are commonly avoided, as every rational number is equal to a fraction with a positive denominator. Fractions are written as two integers, the numerator, and the denominator, with a dividing bar between them.

Irrational numbers

A real number that is not rational is called irrational. Irrational numbers include √2, π, e, and φ. The decimal expansion of an irrational number continues without repeating. Since the set of rational numbers is countable, and the set of real numbers is uncountable, almost all real numbers are irrational.

Transcendental numbers and reals

The set of all real numbers is uncountably infinite but the set of all algebraic numbers is countably infinite, so there is an uncountably infinite number of transcendental numbers.

Infinity and infinitesimals

In mathematics, an infinitesimal or infinitesimal number is a quantity that is closer to zero than any standard real number, but that is not zero. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another.

Infinity is that which is boundless, endless, or larger than any natural number.

Prime numbers

Prime numbers are the numbers that have only two factors, that are, 1 and the number itself. 

• A number greater than 1 with exactly two factors, i.e. 1 and the number itself is defined as a prime number. In other words, if a number cannot be divided into equal groups, then it is a prime number. We can divide a number into groups with equal numbers of items/elements only if it can be factorized as a product of two numbers.

Natural numbers

In mathematics, the natural numbers are those numbers used for counting (as in "there are eight die on the table") and ordering (as in "this is the eighth largest star system in the city").

• Numbers used for counting are called cardinal numbers, and numbers used for ordering are called ordinal numbers. Natural numbers are sometimes used as labels, known as nominal numbers, having none of the properties of numbers in a mathematical sense.

The most familiar numbers are the natural numbers (sometimes called whole numbers or counting numbers): 1, 2, 3, and so on. Some variations include 0 (cardinality of the empty set, i.e. 0 elements, where 0 is thus the smallest cardinal number) in the set of natural numbers. The term is used to describe both sets, including 0 or not. The mathematical symbol for the set of all natural numbers is N.

• In set theory, which is capable of acting as an axiomatic foundation for abstract mathematics, natural numbers can be represented by classes of equivalent sets. For instance, the number 8 can be represented as the class of all sets that have exactly eight elements. Many different representations are possible; all that is needed to formally represent 8 is to inscribe a certain symbol or pattern of symbols eight times.

Integers

An integer is colloquially defined as a number that can be written without a fractional component. 

• The natural numbers form a subset of the integers. As there is no common standard for the inclusion or not of zero in the natural numbers, the natural numbers without zero are commonly referred to as positive integers, and the natural numbers with zero are referred to as non-negative integers.

Real numbers

The symbol for the real numbers is R. They include all the measuring numbers. Every real number corresponds to a point on the number line. Most real numbers can only be approximated by decimal numerals.

Complex numbers

In mathematics, a complex number is an element of a number system that contains the real numbers and a specific element denoted i, called the imaginary unit.

• Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. 

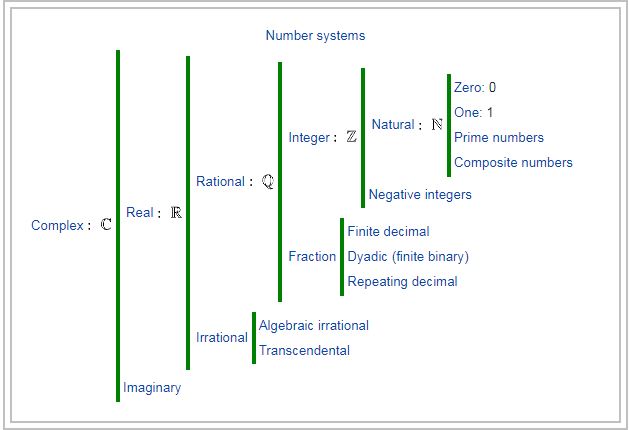
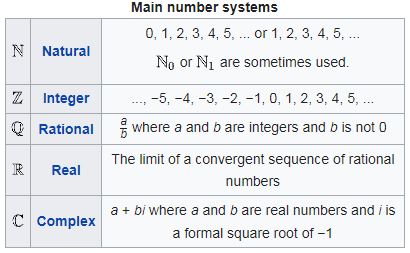
In mathematics, the notion of a number can include 0, negative numbers, rational numbers, real numbers, and complex numbers. Calculations with numbers are done with arithmetical operations, the most familiar being addition, subtraction, multiplication, division, and exponentiation.

• There are many different abstractions that share certain properties of numbers and extend the concept.
• Hypercomplex numbers consist of various extensions or modifications of the complex number system.
• Number systems are considered important special examples of more general algebraic structures such as rings and fields.
• The application of the term "number" can be a matter of convention, without fundamental significance.

Extensions of the concept

p-adic numbers

The p-adic numbers have infinitely long expansions to the left of the decimal point, in the same way that real numbers may have infinitely long expansions to the right. The number system that results depends on what base is used for the digits: any base is possible, but a prime number base provides the greatest mathematical properties. The set of the p-adic numbers contains the rational numbers but is not contained in the complex numbers.

Hypercomplex numbers

Some number systems that are not included in the complex numbers may be constructed from the real numbers in a way that generalizes the construction of the complex numbers. These are called hypercomplex numbers. They include the quaternions H, in which multiplication is not commutative, the octonions, in which multiplication is not associative in addition to not being commutative, and the sedenions, in which multiplication is not alternative, neither associative nor commutative.

Transfinite numbers

For dealing with infinite sets, the natural numbers have been generalized to the ordinal numbers and to the cardinal numbers. The former gives the ordering of the set, while the latter gives its size. For finite sets, both ordinal and cardinal numbers are identified with the natural numbers. In the infinite case, many ordinal numbers correspond to the same cardinal number.

Nonstandard numbers

Hyperreal numbers are used in non-standard analysis. The hyperreals, or nonstandard reals (usually denoted as *R), denote an ordered field that is a proper extension of the ordered field of real numbers R and satisfies the transfer principle. This principle allows true first-order statements about R to be reinterpreted as true first-order statements about *R.

• Superreal and surreal numbers extend the real numbers by adding infinitesimally small numbers and infinitely large numbers but still form fields.